Describe the roles of the Joukowski equation and InfoSurge Pro in surge analysis.
Tutorial resources
These downloadable resources will be used to complete this tutorial:
Surge analysis is an important step in the creation and maintenance of a pipe network, but one that is highly complex. Due to that complexity and the need for specialized analysis tools, many existing guidelines simplify the process.
Most simple expressions, such as the Joukowski equation, only apply in highly restricted or unrealistic circumstances.
For example, two important restrictions must be in place for the Joukowski equation to work:
If conditions are not met, Joukowski equation ceases to be valid, and any conclusions based on it may not be applicable.
Also, Joukowski equation does not consider liquid column separation, or cavitation.
No simplified rules can provide a prediction of worst-case performance under all transient conditions.
Surge response in water distribution systems is sensitive to system-specific characteristics.
Careless generalization and simplification could lead to incorrect results and inadequate surge protection.
InfoSurge Pro is capable of comprehensive surge analysis.
This approach is both justified by its importance and practical, owing to the rapid development of faster computers and efficient numerical simulation models.
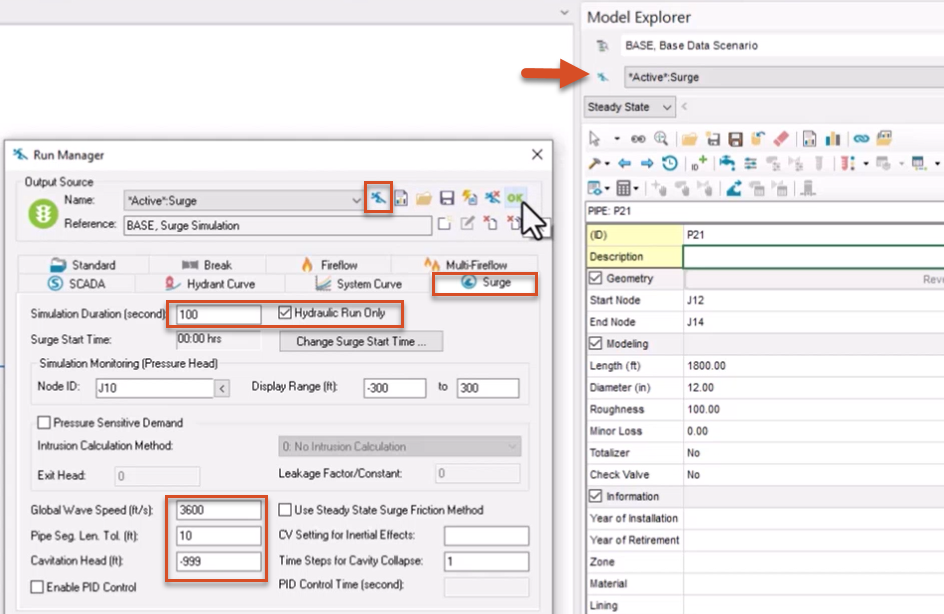
To best understand how InfoSurge Pro performs a surge analysis, it is a good idea to experiment with a simple single-pipe model. This facilitates identification of the various concepts and common procedures involved in running simulations and examining the results.
Cavitation head is the head at which fluid will cavitate. Note that this is a hypothetical value, as it is typically around -33 feet.
In this example, the Pipe Flow is 2663.98 gallons per minute, with a Velocity of 7.56 feet per second.
Note that the Upstream Hydraulic Pressure is 3.86 psi.
This equation multiplies the change in velocity by the pipe wave speed, and then divides this number by gravity, resulting in the change in hydraulic head, in feet. The final calculation, to convert this head value to pressure, is to divide by 2.31.
For this example, the simulation calculates results as a steady state, so the velocity 7.56 feet per second is used. The selected pipe does not have a wave speed, so the global wave speed of 3600 feet per second is used. To maintain the correct units for these calculations, gravity is 32.2 feet per second squared. Using these numbers, the final calculation for the potential surge pressure is 365 psi.
Valve V1 is a surge Active Valve (AV), assigned a stem change curve that closes the valve within 10 seconds. To view the upstream pressure profile of the valve:
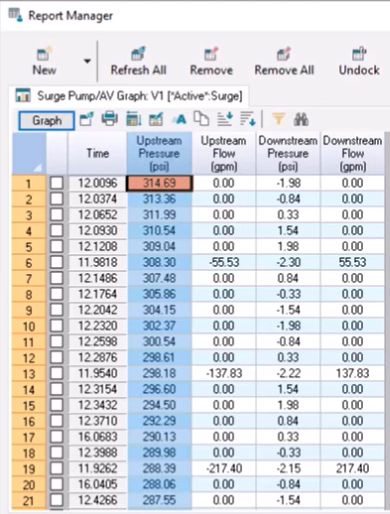
In this example, the maximum surge pressure upstream peaks at 314.69 psi.
Now, change the closure time of valve V1 to see how it impacts results.
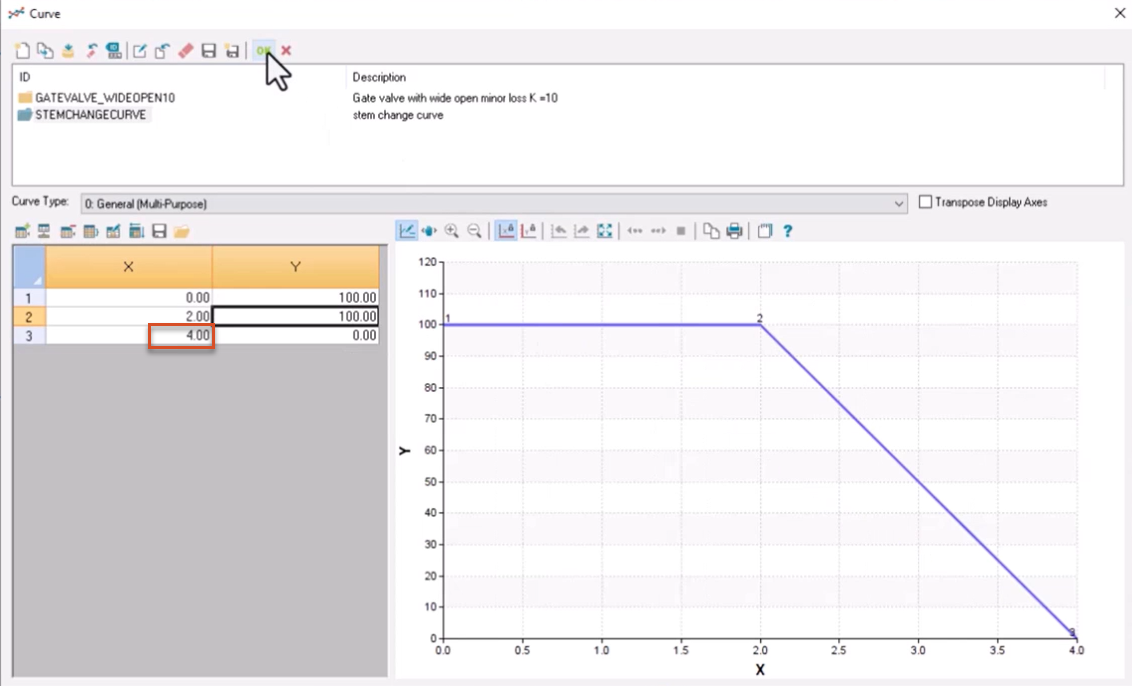
This decreases the valve time from 10 seconds to 2 seconds.
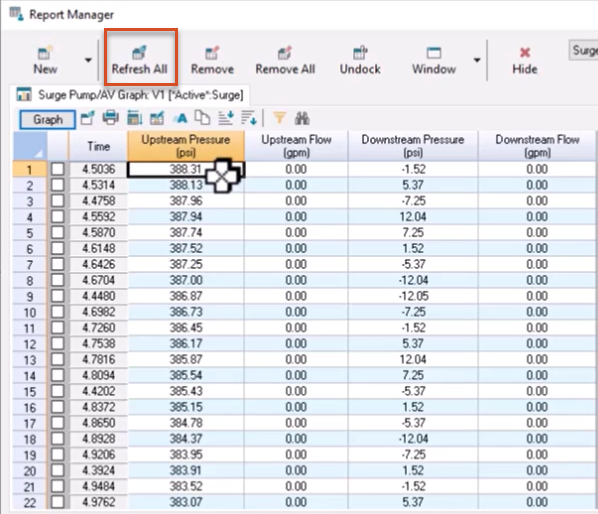
With the decrease in closure time, the maximum upstream pressure increased to 388.31 psi.
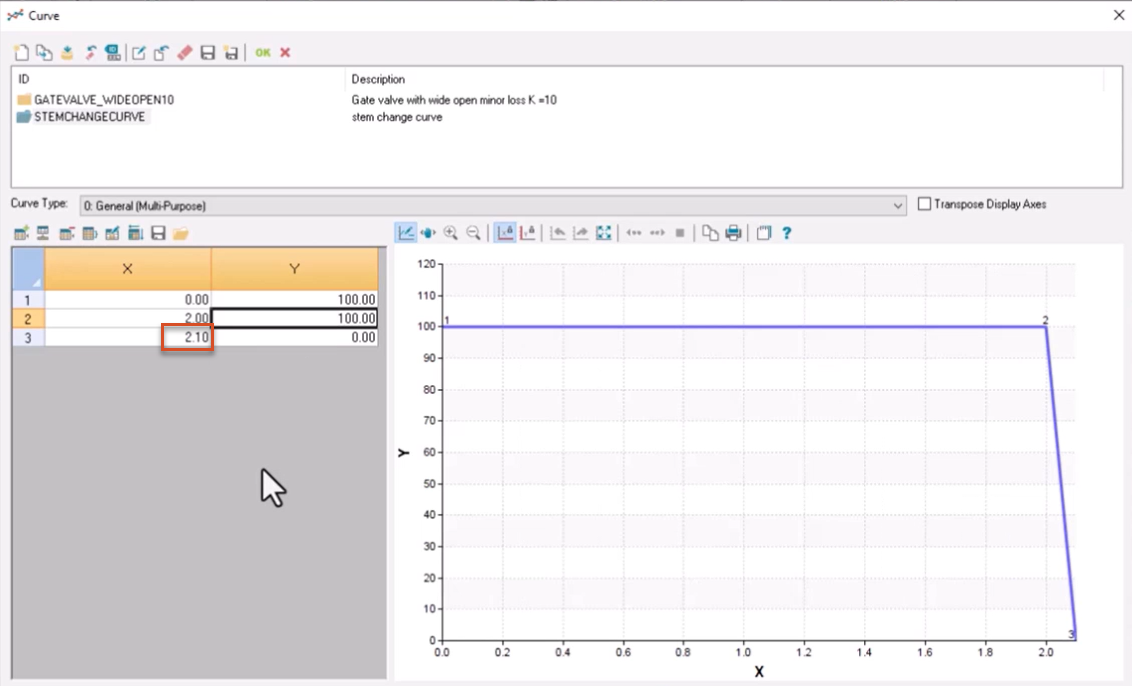
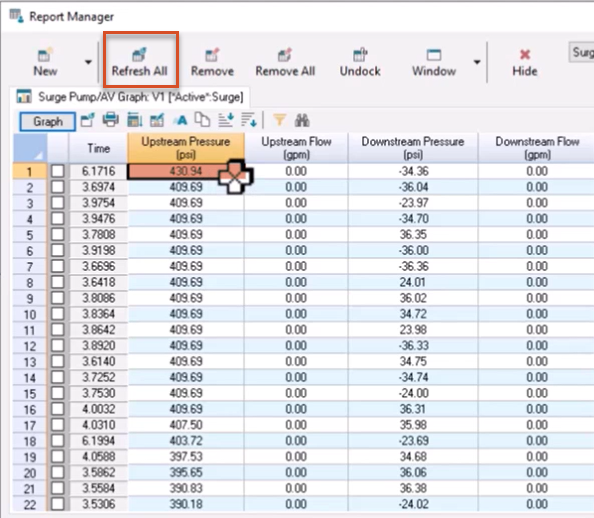
In this example, the maximum upstream pressure increased again to 430.94 psi.
Try making various other changes to the network and perform additional runs to see how they impact results.
To simulate the effect of changing the pipe segment length tolerance:
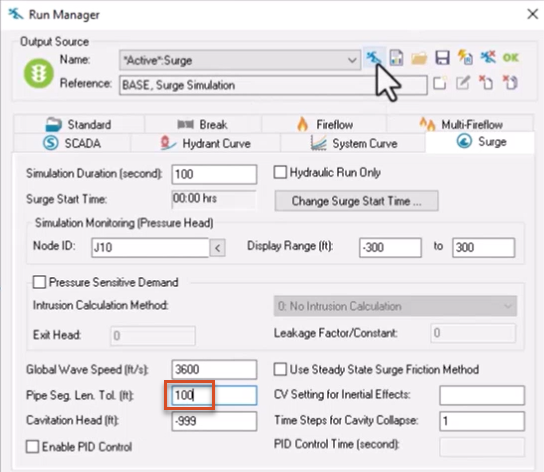
Generally, the larger the pipe segment length tolerance value, the longer the run takes to complete.
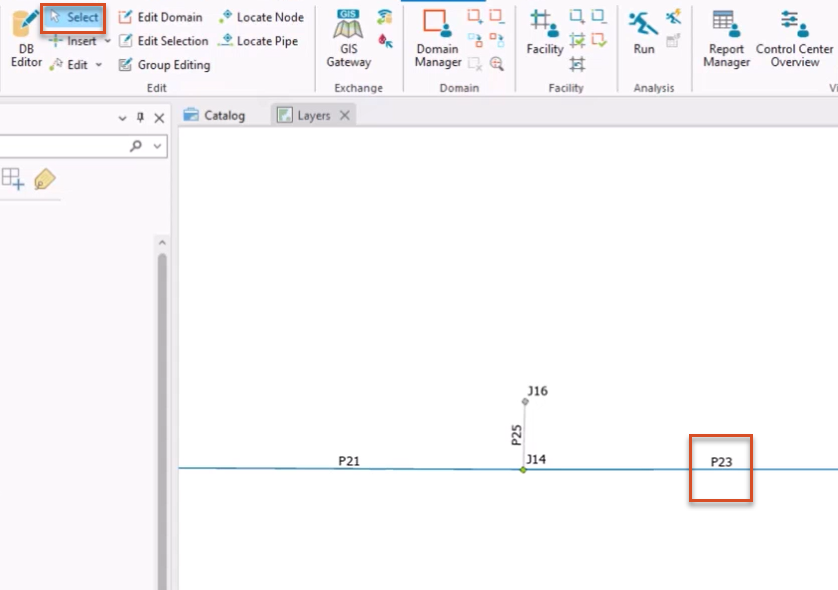
To simulate a dead end wave reflection:
Observe that both junctions have a static pressure of 23.59 psi.
In this example, the pressure at J16 is higher than it is for J14. Because J16 is a “dead end,” the transient wave is reflected here at twice the pressure head of the original wave.
To simulate how friction impacts pipe flow over time:
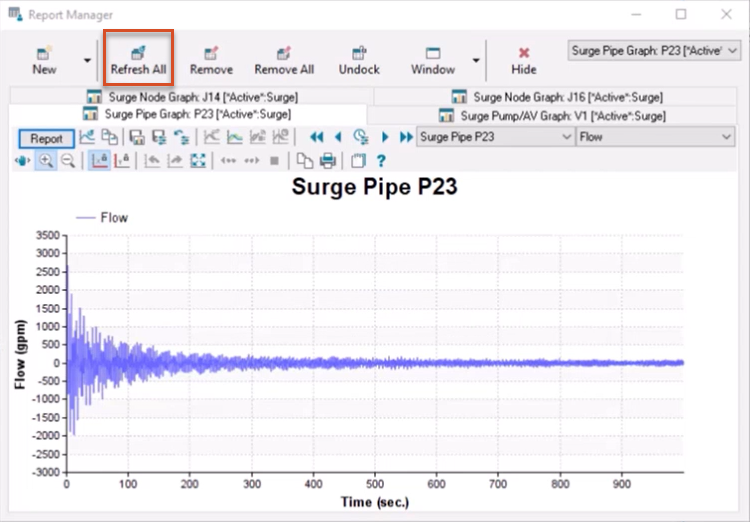
Note that by viewing results over a greater time, the pipe flow eventually approaches a steady state.
To simulate a cavitation event:
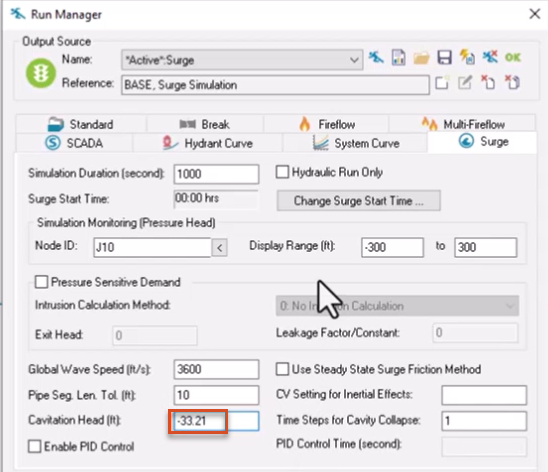
Note that the surge pressure does not approach 0 over time. This is because the cavitation head changed from -999 to -33.21 feet, the head at which cavitation typically occurs.
