We investigate whether Pi (π) can actually be used to help compute details related to a river’s path. Is there something special about Pi that can make modeling rivers, bridges, culverts, spillways, levees, floodplain and floodway delineations, stream diversions, channel improvements, and split flows easier?
The constant Pi has been associated with everything from crop circles to the construction of the Egyptian Pyramids. While it might seem like a neat idea that the mysteries of nature can be explained by a mathematical algorithm – like measuring the concentric circles formed by ripples across a pond when something hits the surface of the water – when it comes to calculating a river’s path using Pi, it’s not so straightforward.
A river’s course is influenced by the complex interactions of various factors. Human intervention through infrastructure projects, seasonal weather and extreme natural events such as flooding can all have an effect. Meteorologists can use satellite data, radar, digital elevation models (DEMs), and supercomputers to forecast and measure the weather’s impact on the environment, as well as to analyze river morphology and topography.
So, how should we approach the calculation of a river’s path? River path calculations and sinuosity measurements are often performed at the basin scale, considering the entire watershed area.
Introduction to river dynamics
River dynamics is the science of understanding how rivers move, change, and shape the landscape over time. At the heart of this field is the study of the stream channel – essentially, the path a river carves as it flows from one point to another. One of the most important ways to describe a river’s behavior is by looking at how much its channel deviates from a straight line. This is where the concept of sinuosity comes in.
Sinuosity is calculated as the ratio of the actual channel length of a river to the straight line distance between two points – typically the river’s source and its mouth. If a river followed a perfectly straight path, its sinuosity would be 1. However, most rivers are not straight; they meander, creating bends and curves that increase the channel length compared to the shortest path between the end points. High sinuosity channels, such as those found in meandering rivers, can have a channel length that is significantly greater than the straight line distance, resulting in a higher sinuosity value.
The degree of meandering and the resulting sinuosity are influenced by a variety of factors, including the river’s flow, the slope of the land, and the characteristics of the soil and bed material. High sinuosity channels tend to develop in areas where the river has the freedom to migrate and reshape its path, leading to complex flow patterns and dynamic changes in the river’s direction. In contrast, rivers with low sinuosity are more direct, with less deviation from the straight line, and often exhibit faster, more focused stream flow.
Understanding the ratio between channel length and straight line distance is essential for analyzing river behavior, predicting future changes, and managing natural resources effectively.
Is there a calculation for a river’s path or straight line distance from point A to point B?
Calculating a river’s path typically involves factors such as topography, terrain, elevation, and hydrological principles combined with the analysis of geographical and geological data.
Rivers flow based on physical forces like gravity, elevation differences, and the shape of the landscape. Geographic Information Systems (GIS) and hydrological models made with apps like Autodesk’s own InfoWorks ICM are often used to simulate and predict the course of rivers based on these kinds of factors. The determination of sinuosity is a key step in river analysis and management, providing important insights for ecological and hydromorphological studies. Does the app do it by embedding a Pi-based formula?
It is possible to measure the bends and turns of a river with a simple formula which divides the length of a river’s course by the straight-line, direct distance between its start and end points (as the crow flies). In this context, the straight-line distance is referred to as the shortest path length, and it serves as the denominator in the calculation.
The resulting measurement is referred to as ‘sinuosity’ – a totally straight river would have a sinuosity of 1, for example, while a very bendy river will have a higher sinuosity. Sinuosity values can also be estimated using GIS data and remote sensing techniques, though these methods may have certain limitations.
What is sinuosity?
Referencing the ability to curve or bend easily and flexibly, and often used to describe streams and rivers in geography and geomorphology, sinuosity provides a useful metric for calculating how much the path of a river deviates from a straight line over a certain distance. River curvature is a key aspect of planform analysis and is closely related to sinuosity, as it helps describe the shape and behavior of the river channel.
In other words, it quantifies the degree of meandering or winding across a river’s course, often expressed in terms of the degrees of curvature or bending along the river path. The sinuosity of a river can be calculated by measuring a river’s actual meandering channel length and dividing it by the straightest route, as the crow flies, from its source to its mouth.
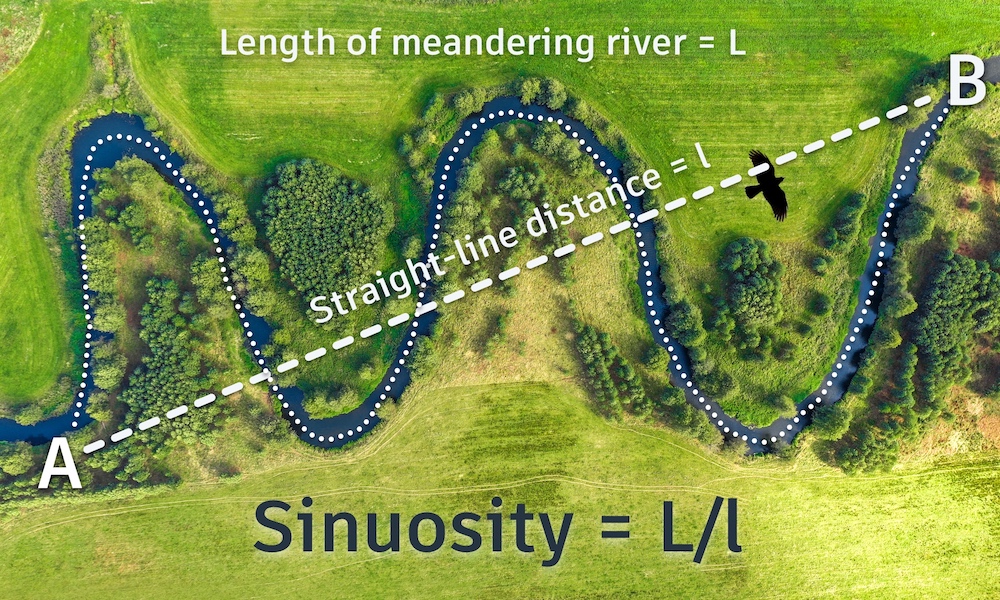
The resulting sinuosity value can vary widely based on the characteristics of a river and the landscape it flows through. A sinuosity value of greater than 1 indicates a meandering river. For example, a sinuosity value of 1.5 would mean that the river’s actual course is 1.5 times longer than the straight line distance between its start and end points.
According to mathematician James Grime, who wrote about this topic in The Guardian, “a very bendy river can have very high sinuosity with no limit to how high it can go.”
Sinuosity is an important parameter to understand how a river interacts with its surrounding environment. It’s influenced by factors such as the geological composition of the land, the gradient of the terrain, the river’s discharge, and the sediment transport within the river. The function of sinuosity includes supporting diverse aquatic habitats, influencing river dynamics, and contributing to the overall stability and resilience of the stream system.
High sinuosity rivers tend to have more pronounced meanders and may change their course more frequently over time, while low sinuosity rivers are relatively straight and stable.
Pi me a river
It has been claimed that the average sinuosity of rivers around the world is Pi… If true, this would mean that rivers are typically just over three times longer than the straightest route from source to mouth with an average sinuosity value equating to Pi (~3.14).
This theory was explored in a 1996 paper published in the journal Science. Entitled River Meandering as a Self Organization Process, Hans-Henrik Stølum used simulations and empirical data to show a meandering process that “self-organizes the river morphology into a critical state”. Foundational work by Leopold et al. established key principles of channel sinuosity and river morphology, providing the scientific background for such modeling studies.
Stølum justified his research with fractal geometry – the theory that if the bends of a river can be compared with arcs of circles, and the little curves of a river by arcs of smaller circles, then the sinuosity of the river can be calculated to be Pi. These analyses are typically performed on a two-dimensional plane, where the river path is projected and measured. His study found that sinuosity varied between a low of 2.7 and a high of 3.5. His work didn’t identify a golden ratio for rivers, but it is an intriguing theory.
One point not in his favor: A more recent crowdsourced data project failed to replicate Stølum’s Pi average and was ultimately too small to prove or disprove a theoretical model for Pi calculating the total average of all the world’s rivers. After analyzing 258 rivers, it recorded an average sinuosity of 1.94. In such studies, researchers attempt to match modeled sinuosity values to observed river data to validate or refine their models.
One of Einstein’s other theories
While the mathematical constant Pi has applications in geometry and physics, it isn’t directly used to determine a river’s path. The mathematics involved are more related to fluid dynamics and the laws of physics than to the use of a constant like Pi.
Like ancient mathematicians before him who found the concept of irrationality maddening, Albert Einstein refused to believe in the inherent unpredictability of the world and was among the first to ponder Pi’s capabilities with regards to calculating river flows. He used fluid dynamics and chaos theory to show that rivers tend to bend into loops.
Einstein explained how helical flow develops in a meandering river, and that because the higher-velocity portions of the stream will be driven to the outside (concave) portion of the river bend, erosion will be greater there. He noted that because the helical flow possesses inertia, the circulation (and the erosion) will be at their maximum beyond the inflection of the curve.
Hence, the waveform of the river will migrate in a down-current direction. Meander migration is a key process in river evolution, as the continuous shifting of bends shapes the channel planform and influences the development of sinuosity over time. Finally, Einstein explained that the larger the cross-sectional area of a river, the slower the helical flow will be absorbed by friction; which explains why larger rivers have meander patterns with longer wavelengths.

As Grime notes, erosion causes bends in rivers to become more extreme, which increases a river’s sinuosity. However, features such as bedrock outcrops, sediment deposits, or log jams can act as forced elements, constraining or redirecting the natural course of the river and altering its meander patterns. Nature then takes its course as a river aims to correct itself with the water taking a shortcut and cutting off the bend to form an oxbow lake, lowering a river’s sinuosity. It was during his study of this oscillation that Stølum first noticed the value of Pi.
The length along the river of the meander is like the circumference of a circle, while the straight-line distance from one bend to the next is diameter-like. Hence, it makes sense that the ratio of these lengths would appear Pi-like. But the truth is a bit less straightforward.
During high flow events, such as floods, water levels rise, allowing the river to access its floodplain, which can reduce downstream flooding and promote stream stability. Ultimately, while there is evidence of natural mathematical phenomena at play in how rivers evolve, their course is influenced by many competing factors that one algorithm alone can’t explain.
Applications and implications
The study of river dynamics and channel sinuosity has far-reaching applications in fluvial geomorphology, environmental science, and engineering. For example, understanding the sinuosity of a river is crucial for predicting flood risk and designing floodplain management strategies. High sinuosity channels, with their winding paths and frequent bends, can slow down stream flow and help dissipate energy during high water events, reducing the risk of downstream flooding.
In ecology, the complexity of meandering rivers and high sinuosity channels creates a diverse range of habitats, supporting a greater variety of aquatic species. The bends and curves of a sinuous river can lead to the formation of pools, riffles, and backwaters, all of which are important for fish, invertebrates, and plant life. This makes channel sinuosity a key factor in river restoration projects and the conservation of natural resources.
From an engineering perspective, understanding the self organization process of rivers—how flow, sediment, and channel morphology interact to create complex patterns—can inform the design of infrastructure such as bridges, culverts, and levees. For instance, recognizing that high sinuosity channels are more likely to migrate or change course can help engineers plan for long-term stability and reduce maintenance costs.
Sinuosity also plays a significant role in the transport and trapping of pollutants and sediment. In high sinuosity channels, the slower, more variable flow leads to greater deposition of sediments and more efficient trapping of pollutants, which can improve water quality downstream. This process is a prime example of how the natural dynamics of a river can lead to beneficial outcomes for both people and ecosystems.
Challenges and limitations
While measuring and understanding river sinuosity is essential, it comes with its own set of challenges and limitations. One of the primary difficulties lies in accurately determining the channel length and the straight line distance between two points, especially in remote or densely vegetated areas where direct access is limited. The presence of river bends, log jams, and channelization can further complicate the measurement of the flow path, as these features can alter the river’s course and create deviations from the expected line.
Sinuosity is not a static value—it can vary significantly over time and across different sections of a river. Seasonal changes, extreme weather events, and human interventions can all cause the channel length and flow path to shift, making it difficult to predict future changes with precision. The use of digital elevation models (DEMs) and remote sensing technologies has improved our ability to analyze river channels from a distance, but these methods are sensitive to the resolution and quality of the data. Small errors in the digital representation of the landscape can lead to significant inaccuracies in the calculated sinuosity.
Additionally, factors such as channelization (the artificial straightening of rivers), the formation of new river bends, and the accumulation of debris like log jams can all influence the measured sinuosity and the actual flow path of the river. These complexities mean that a single measurement or model may not fully capture the dynamic nature of river systems.
To address these challenges, researchers and practitioners often combine field measurements, remote sensing data, and advanced modeling techniques to obtain a more comprehensive and reliable understanding of river sinuosity. By considering the limitations and variability inherent in river systems, we can better predict, manage, and protect these vital natural resources.
Geek out on water with us
- Studying to become an engineer? You’ll want to know about this: Autodesk Water Infrastructure products now available to students and educators around the globe – for free.
- How do engineers model floods? Learn about HEC-RAS: Its history, benefits, drawbacks, and alternatives.
- Subscribe to the One Water blog newsletter and fill up on innovative and interesting water trends – in particular things that are related to sustainability.